2  Research objectives

In this chapter, we will take a look at objectives of empirical work. Section 2.1 will be concerned with the kinds of inferences that are often made when using data for scientific purposes. We will present a classification of inferences along two dimensions. This delineation gives us a better idea of the role played by statistical inferences in research work. It also serves to inform our discussion of statistical modeling and model specification in later chapters. Section 2.2 then considers the topic of generalization.

2.1 Inferences from data

An important part of research work involves the use of empirical observation to make inferences. According to Merriam-Webster, the word inference denotes “the act or process of reaching a conclusion about something from known facts or evidence”. In the following, we will distinguish between different kinds of conclusions that are often made by researchers. The kind of inferences that are made depend on the objectives of the researcher.

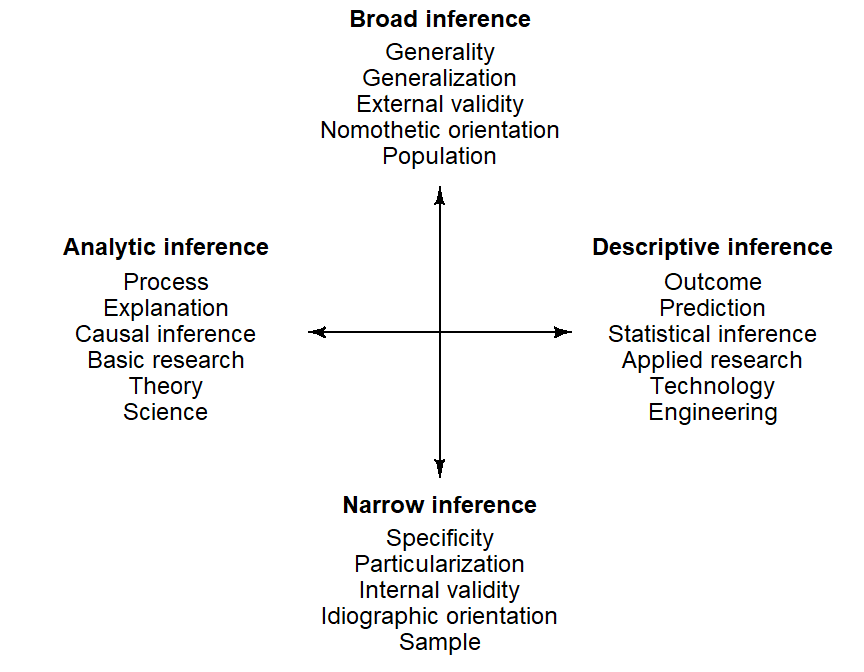
For our present purposes, we will classify inferences along two dimensions, which are shown graphically in Figure Figure 2.1. The horizontal dimension is concerned with the type of inference, largely distinguishing between the numerical description of the observed data (descriptive inference) and the substantive explanation of patterns in the data (analytic inference). The vertical dimension marks the scope of inference, the breadth of validity that is attached to a conclusion – here, we may distinguish between broad and narrow inferences. The endpoints of each continuum list related concepts and ideas. We now take a closer look at the two dimensions.

Figure 2.1: Classification of inferences, Type of inference (vertical dimension) and scope of inference (horizontal dimension). The diagram is adapted from N. H. Anderson (2001, 9) and complemented with terminology used by different authors to refer to similar notions (see text for details).

2.1.1 Type of inference

…
  • Language data (Evert 2006; Baroni & Evert 2009)
  • Descriptive inference: Extensional view of language – “language as an infinite body of text, comprising all the utterances that have ever been made or will ever be made by the relevant group of speakers” (Evert 2006: 179)
  • Analytic inference: Intensional view of language – Competence of human speakers, the properties of language as a formal system
  • E-language vs. I-language (Chomsky 1986: Knowledge of language: Its nature, origin, and use.)
  • extrastatistical inference: Wilk & Kempthorne 1955 (cited in Anderson 1961: 312)

The distinction along the vertical dimension contrasts two fundamentally different types of conclusions that can be made based on data. The first kind, which we refer to as descriptive inference, is a statement about some quantity of interest (e.g. a percentage or some other average score). This type of inference focuses on the outcome quantity which may, in certain practical applications, be of direct interest. Descriptive inferences are typical of applied research, where findings often inform real-world decisions and serve as a basis for action. A central concern is therefore the predictive accuracy of the result at hand, i.e. whether we can make sufficiently accurate predictions for unobserved cases or future outcomes. Descriptive inference can rely on statistical theory – tools such as p-values and confidence intervals are statistical uncertainty statements about the inferred or predicted outcome quantity.

The second kind of conclusion we can make based on data is an analytic inference. It is not primarily concerned with numbers, but rather with their conceptual interpretation and substantive meaning. We seek a deeper understanding of patterns in the data, and try to offer an explanation for our observations. Interest is therefore in the kind of process or mechanism that generated the data – why these patterns emerge and how they came about. This kind of conclusion, which is necessarily tentative, reflects our scientific interest in the underlying system, or forces, that are mirrored in the observed data. Natural language use – as documented in corpora – reflects language-internal forces (e.g. cognitive constraints, language universals) and language-external ones (e.g. social factors). Analytic inference is therefore concerned with explanation or causation rather than description or prediction, and is typical for basic research with a theoretical orientation. Depending on the research context, the notion of a process may refer to a mechanism or operation in the real world (as in industry) or in the conceptual, theoretical world (such as cognitive constraints). For analytic inferences, statistical theory is of no direct help. Rather, such inferences are extra-statistical – they rely on knowledge of the subject matter.

Let us consider some linguistic examples of each type. Descriptive inference, with its focus on a measured quantity and (possibly) its predictive accuracy, is typical of certain forms of language data work. For instance, descriptive grammars or dictionaries may include quantitative information on certain questions of language use. Examples are (i) the usage rate of coordinators in initial position (Biber et al. 1999, 84), (ii) the positional distribution of adverbials (Quirk et al. 1985, 501), and (iii) the pronunciation of words (e.g. schedule) across varieties and age groups (Wells 2008, 717). Other areas that rely on descriptive inference include applied linguistics, e.g. the comparative evaluation of teaching methods, and certain domains of natural language processing, e.g. the development of automatic taggers or translation tools. In all these applications, the interest is restricted to the outcome quantity (e.g., for schedule, the preference of /sk-/ /∫-/, expressed as a percentage) or the predicted outcome (e.g. the most likely part-of-speech tag for a given form).

Analytic inference, on the other hand, is typical of work with a theoretical orientation. Interest does not primarily center on the specific outcome quantity, but on a deeper understanding of the patterns we see. The focus is on linguistic interpretation. For instance, we may be interested in working towards an explanation for distributional patterns of variants, i.e. different ways of saying the same thing. Examples are the dative, genitive, or comparative alternation in English. We might be interested in whether certain contextual constraints, such as constituent length or animacy, may be operative and incline the speaker towards one variant over the other. Further examples include the psycholinguistic notions of frequency effects (e.g. type and token counts as clues to the differential productivity of morphological patterns) and complexity effects (e.g. the use of support strategies to alleviate working memory load).

The distinction between descriptive and analytic inference serves to highlight two important points for empirical research. The first concerns their discordant nature – they are very different research goals. Obviously, both have their merits, and it would seem that, in certain research settings, we would like to pursue both objectives. As N. H. Anderson (2001) [p. 10-11] notes, however, descriptive and analytic inferences require different strategies in study design and data analysis. Analytic inferences rely on restriction and simplification strategies, to isolate the process of interest. A typical example is an experimental study eliciting responses under tightly controlled, artificial circumstances. Descriptive inference, on the other hand, aims for “realistic” observation that is representative of the real-world settings to which research findings are to be applied. The important point is that aiming for both types of inference requires the researcher to make compromises, which may lead to fuzzy inferences. As noted by N. H. Anderson (2001, 10), “[a]ttempts to achieve both goals are likely to achieve neither” (see also Sidman (1960), p. 194]. The second essential point that is clarified by the distinction between descriptive and analytic inferences is the fact that they rely on very different sources of information and reasoning aids. While descriptive inferences can be formed using statistical procedures, the kind of analytic inferences that are typical of the cognitive and behavioral sciences rest almost entirely on extra-statistical grounds. There are no statistical tests or procedures that allow us to attach uncertainty intervals to our inferences. These kinds of research conclusions hinge on experience and judgement – they are backed by knowledge of the subject-matter and research area.

Corpus data and analytic inferences

The question of whether corpus data can be used to make inferences on speakers’ underlying grammars has received some attention in the literature (e.g. Arppe et al. 2010; Baayen and Arppe 2011; Divjak, Dąbrowska, and Arppe 2016; Divjak and Arppe 2013)

In variationist corpus analyses, regression analyses produce a set of probabilistic weights that attach to the predictors studied.[^We will use the label predictor or factor to refer to a variable that is assumed to show an association with the outcome. A predictor or factor can be continuous or categorical. Our usage of the label “factor” contrasts with the terminology used in variable rule analysis, where a categorical factor (or predictor) is referred to as a “factor group”, the label “factor” being used to denote the individual categories. In accordance with standard statistical terminology, these categories will here be referred to as predictor or factor levels .] A key question for linguistic interpretation is what meaning should be given to these probabilistic weights. We may contrast two extreme views on the matter: the naïve and the skeptical view. First, the naïve view, understands the set of probabilistic weights as a direct reflection of the underlying grammar. Regression coefficients are then assumed to have directs analogues in the mind. This reification of regression coefficients was perhaps characteristic of early variationist research (e.g. Cedergren and Sankoff 1974). It was criticized early on by Bickerton (1971, 461), who noted the need to name a “recognizable mental process”. This criticism was readily adopted by variationists. Sankoff (1978, 235–36) concedes that “the regularities and tendencies modeled by these probabilities are of different kinds and come from different sources”, and that the probabilistic weights are “simply quantitative generalizations”, “analytical abstractions rather than components of language” (Sankoff 1978, 235). Likewise, Sankoff and Labov (1979, 217) state: “we do not make the error of confusing the set of rules we write with the grammatical processes that people use.”

The skeptical perspective, on the other hand, questions the cognitive plausibility of these probabilistic weights, on the grounds that the way they are derived from data is at odds with principles of human cognition and learning.

…
  • “how to understand the statistical results from a cognitive perspective” (Baayen and Arppe 2011, 8)
  • characteristics of mental grammars
  • linguistic cognitive processes
  • linguistic knowledge that is represented in the brain
  • “characteristics observable in language usage reflect characteristics of the mental processes and structures yielding usage, even though we do not know the exact form of these mental representations”
  • posited underlying language system governing usage
  • Divjak and Arppe (2013, 229–30, 235–37)
  • Klavan and Divjak (2016) consider the cognitive plausibility of corpus-based models. They consider a model to be cognitively plausible if it shows the same predictive ability as humans. This is a very global assessment and fails to consider deeper questions, such as whether the prediction weights bear any realism.
  • Uniformity of mental grammars? Divjak, Dąbrowska, and Arppe (2016, 27) note that due the characteristic multicollinearity of variables (and resulting redundancy), speakers may in fact have internalized different grammars that nevertheless arrive at the same production behavior. (some references to be found there)

2.1.2 Scope of inference

A second dimension along which inferences vary is their scope, which refers their range of validity. Studies are typically based on a limited set of entities, i.e. a sample. The basic distinction here is whether interest is restricted to the sample of entities at hand, or whether the aim is to extend the breadth of interpretation beyond the cases at hand. The scope of inference, sometimes referred to as th inference space (V. E. Anderson and McLean 1974, 57) Accordingly, we may distinguish between narrow inference and broad inference1. The label “entities” can refer to different, sometimes co-occurring classes of units in our study – speakers/texts, words, languages, varieties, or (micro)genres. Within a single study, the intended scope of inference may therefore vary for different classes of units.

1 We adopt these terms from (McLean, Sanders, and Stroup 1991; see also Stroup 2013, 70, 90–99)

We will use the term narrow inference to refer to situations where inferences are made only concerning the set of entities studied. Thus, we could decide to restrict our statements to the particular set of genres represented in our data, to the selection of words we happened to obtain, or even to the specific set of individuals we observed. Our statistical conclusions would then be specific to this narrow set. The entities that form the target of narrow inference assume a special status, since our deliberate restriction in scope can sharpen our knowledge about these individual units. A focus on individual speakers (or writers) corresponds to an idiographic research perspective Windelband (1998). Since language resides in the individual speaker’s mind, there is clearly some merit to this approach to linguistic study. From a statistical perspective, the modesty of our inferential ambitions is awarded with more accurate estimates, i.e. narrower uncertainty bounds around our key quantities.

The term broad inference, on the other hand, will be used to refer to situations where we use our sample as a stepping stone to make statements about the populations of entities that this sample represents. We then make generalizations based on our sample data. Questions of external validity then arise – that is, to what extent can we extrapolate these findings to unobserved entities. The individual entities are then used to form summary measures (such as averages), which are then used as estimates of population features. This entails a shift from an idiographic to a nomothetic perspective Windelband (1998), a more general level of description, which averages over individual and unique entities. Statistical theory offers tools to compute and express the additional uncertainty resulting from the extrapolation to unobserved entities. However, the adequacy of these methods hinges on certain requirements. Thus, statistical theory only offers guarantees of adequate performance if the sample of entities at hand is a random sample from the underlying population. Since this is rarely the case in everyday research, broad inference from non-random samples is to some (perhaps a considerable) extent extra-statistical and therefore relies on knowledge about the research area.

The distinction between broad and narrow inference highlights two aspects of empirical research. First, how wide to span the inference space is a decision made by the researcher. Broad inference is an optional move: We can deliberately restrict the intended level of generality of our research findings. This may be a good call if the data at hand do not offer the type and/or amount of information that is necessary to derive adequate uncertainty bounds for broad-inference estimates. Thus, in sparse data settings, broad inference yields but a very blurry picture of generalized patterns, perhaps too blurry to be of any use. In other settings the data may not include information about certain sources of variability that would be needed to determine the uncertainty surrounding our statistical projections. Sometimes, then, the data provide a weak or unreliable inductive base for broad inference, which would prompt a circumspect researcher to backtrack and rely on narrow-inference estimates. It is also not difficult to imagine settings where both types of estimates may be combined. The second aspect of empirical research that is highlighted by the inference space is the difference between statistical and extra-statistical sources of information for drawing inferences.

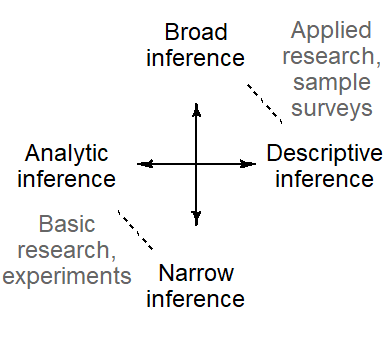
2.1.3 Type and scope of inference: Co-occurrence patterns

There is a tendency for the type and scope of inference to show an association in particular research settings. Typical connections are shown in Figure Figure 2.2). Basic research, with its purely scientific, theory-oriented approach aimed at understanding causal systems, shows a tendency to resort to narrow inference (Mook 1983; Cox 1958, 10–11). Methodologically, this research style relies on experimentation and randomization schemes for the isolation of causal forces. Applied research, on the other hand, serves as a basis for action or decisions in the real world. It shows a more pronounced interest in the representativeness of the observations under study and in the applicability of conclusions to new conditions and circumstances. Statistical techniques that feature prominently in this branch of science are survey sampling and random sampling schemes.

Figure 2.2: Co-occurrence tendencies of type and scope of inference.}
  • See also Rabe-Hesketh and Skrondal (2021), p. 100-102: In the survey-sampling literature, analytic inferences about the data-generating mechanism are referred to as superpopulation inference (or infinite population inference) since even an exhaustive sample still represents only a sample from the data-generating model. Descriptive inferences about finite population parameters only need to take into account sampling variability. Such inferences take into account design features and are therefore called design-based inferences. In contrast, model-based inferences target parameters of the data-generating mechanism. Note however, that the mechanism does not refer to a genuine scientific causal mechanism, rather a descriptive mechanism.

2.1.4 Type and scope of inference: Literature

Discussions of different types and scopes of inference appear in many places throughout the literature. Figure Figure 2.1) is adapted from N. H. Anderson (2001, 9). He refers to the illustration as a validity diagram and labels the vertical ends “outcome” and “process”, and the horizontal ends “internal” and “external”. This distinction is helpful since it distinguishes two conceptually distinct dimensions, which are sometimes mixed to varying degrees by other writers.

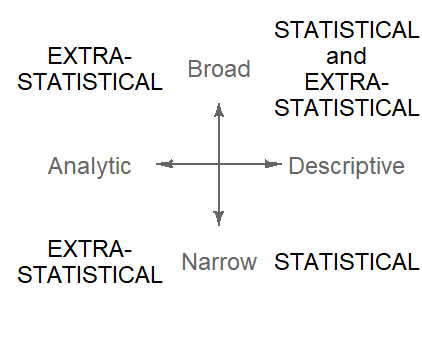
Thus, in the domain of industrial experimentation and quality control, Deming Deming (1975) introduced the distinction between enumerative and analytic studies, the vertical dimension in Figure Figure 2.1).2 This distinction was formulated with applied contexts in mind, where research findings serve as a basis for action – in the words of Mook (1983, 380) “a real-life setting in which one wants to know what to do”. Examples are medicine, public service and industry. A criterion that helps distinguish between enumerative and analytic tasks is the notion of a 100% sample (Deming 1975, 147). If we were able to do an exhaustive analysis of the population of interest, we would have the perfect state of information about the population. If our interest were, instead, in a process that produced certain patterns in the data (and the population), our knowledge of this process would still be incomplete. Deming Deming (1975) does not distinguish between internal and external validity; rather, the focus is on applications where the aim is to generalize (see also Gitlow et al. 1989).

2 Hahn and Meeker (1993), p. 4 take a broader view of analytic studies as research that “is not dealing with a finite, identifiable, unchanging collection of units, and, thus is concerned with a process, rather than a population”.

In the field of psychology, on the other hand, large parts of the discussion center on the distinction between a process-based and a population-based interpretation of statistical inference Frick (1998), again referring to the vertical dimension in Figure Figure 2.1). Here, analytical inferences (process model) are linked to questions of internal validity, whereas descriptive inference (population model) are intertwined with questions of external validity.

2.1.5 Implications for language data analyis

How do these settings differ from typical corpus-linguistic applications? Most corpus-based work is concerned with learning about language, its use and acquisition. That is, the interest is typically theoretical. Our findings do not inform real-world decisions. Rather, the data we collect serve to provide some insight into the workings of language. This is not to say that generalizability to a specific population is irrelevant. We do, however, need to think about which kind of generalization we wish to make.

Observational studies fall in between the two poles (Kish 1987, 20)

2.1.6 Statistical vs. extra-statistical reasoning

We have just distinguished different kinds of inferences that research workers are often interested in making. Let us now summarize to which extent inferences can be made on statistical grounds.

It turns out that statistics is relevant only for certain inferential tasks. Analytic inferences, for instance, are outside the purview of statistical methods. While quantitative tools may provide aids for the reasoned interpretation of data, there is no way of attaching statistical uncertainties to the truth value of a scientific explanation. Even experiments do not produce genuinely analytic inferences. They allow us to infer causal relations, which, however, remain at a descriptive level. A distinction is therefore sometimes made between causal description and causal explanation. In general, then, analytic inferences rest on subject-matter grounds.

Descriptive inferences, on the other hand, can be made on statistical grounds. Narrow inferences are restricted to the set of conditions and contexts actually observed, and the data at hand therefore (usually) provide ample grounds for narrow descriptive inferences. In making broad inferences, on the other hand, we wish to extend our conclusions to unobserved settings and circumstances. The degree to which the data at hand can buttress these extrapolations cannot be answered on statistical grounds. It is a matter of judgement and hinges on our knowledge of the research area and the empirical experience we have accumulated (Sidman 1960, 59; MacKay and Oldford 2000, 276).

Figure 2.3: Scope and type of inference: Statistical vs. extrastatistical reasoning.

2.2 Generalization

2.2.1 Generality of what?

from Sidman (1960: 46-47) - Which aspect of the data does one wish to test for generality? - With which features of the data are we particularly concerned? - Generality of what? - Which type of generality do we wish to determine? - Directionality of effect - Functional shape, shape of distribution - Quantitative values

the current state of development of the science.

2.2.2 Levels of generality

Since generalizations can be made at different levels of descriptions and analysis, the distinction between broad and narrow inference can be made at different levels. Figure Figure 2.4) (adapted from Runyan (1982, 7)) provides a sketch of certain layers of generality.

Generalizations applying to specific individuals. Let us start at the bottom by first considering the individual speaker. Thus, we may obtain a certain amount of spoken or written material produced by this individual. This excerpt is a sample from their language use, and may serve as a basis for inferences about the general patterns of language use, or the mental grammar, of this speaker. At this level of analysis, broad inference would target the linguistic system of this individual, from which we have observed a limited amount of output.

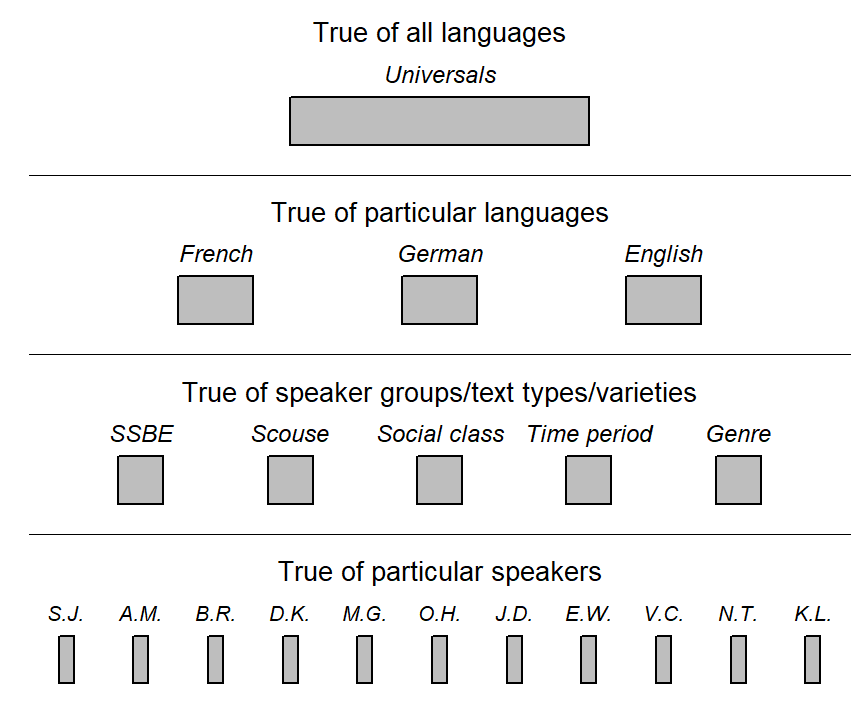
Figure 2.4: Broad vs. narrow inference for speakers, speaker groups and communicative situations: Levels of generality. Adapted from Runyan (1982, 7).

Group-specific generalizations. At a higher level of analysis, we might be interested in the linguistic behavior of a particular socio-demographic subgroup, say, the speech of London teenagers. Let us assume we have data from 15 speakers. Broad inferences are generalizations to this speaker group, and the 15 individuals serve to inform our summary measures about this population, i.e. London teenagers in general. If we instead decide to restrict the generality of our statements to the 15 speakers at hand, this would constitute a shift to narrow inference.

Language-specific generalizations. Inferences may aim for even broader levels of validity, for instance a particular language. For Present-Day spoken British English, for instance, socio-demographic subgroups would then be considered as a sample, informing conclusions at the more general level. For written language use, on the other hand, individual genres could be considered as a sample of a larger population. Depending on the focus of our study, our interest may center on these broad inferences, i.e. average trends across subgroups or genres; however, our linguistic attention could also be focused on these lower-level units, in which case we would be interested in making narrow inferences.

Universal generalizations. We can pursue still broader generality by trying to identify language-universal features. Such generalizations across languages would concentrate on features common to all natural languages. These may result from shared functional-cognitive constraints, or, depending on the theoretical viewpoint adopted, innate architectures.3 At this highest level of linguistic generality, a sample consists of a set of languages, which inform our generalizations.

3 Note that the question of what gives rise to commonalities between languages are answered by analytic inferences.

As these examples illustrate, the scope of inference is relative; it depends on the descriptive level at which generalizations are advanced. Regularities may be found at each level, and our research objectives identify the tier at which (or to which) we wish to generalize. Lower-level units then usually form the sample that informs higher-level, broad-inference statements. The conceptual relationship between sample and population therefore surfaces at different elevations in Figure Figure 2.4), and the epistemological status of a given unit (i.e. grey box), depends on the linguistic question being asked. A specific language, for instance, may be a broad-inference target, or it could be considered as a unit of analysis that informs generalizations at a still broader level of inference.

So far we have considered generality with regard to speakers, speaker groups, and communicative situations. The scope and levels of inference were oriented towards language-external units of description and analysis. A similar hierarchy may be stipulated for language-internal entities. Figure Figure 2.5) shows increasing levels of generality based on lexical units as the lowest level of generality. The ideas and relationship we have discussed for language-external tiers of generality directly apply to this language-internal system.

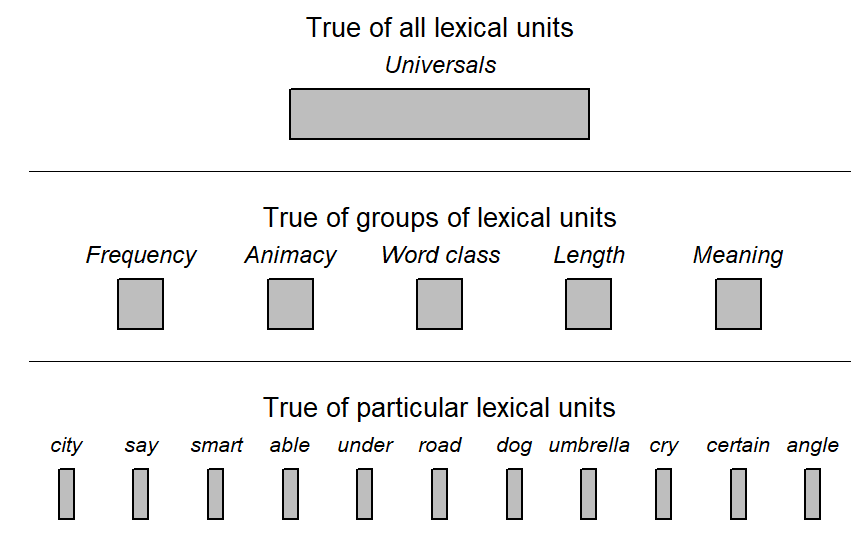
Figure 2.5: Broad vs. narrow inference for lexical structures: Levels of generality. Inspired by Runyan (1982, 7).

To recapitulate, there are different levels at which identify regularities and advance generalizations. Two pyramidal constellations, with different altitudes of generality, were sketched: (i) a language-external one, resting on the individual speakers as the lowest-level units, and (ii) a language-internal one , with lexical units constituting the base of the hierarchy. As we move upwards, we extend the scope of inference. Moving the target of inference brings about changes in what exactly constitutes sample vs. population. The distinction between broad and narrow inference, then, is only meaningful if we are clear about the level of generality, both language-externally (Figure Figure 2.4)) and -internally (Figure Figure 2.5)).

Evaluate Shadish et al.’s 4-step ladder of validity

2.2.3 Generalizability Theory

Some basic notions from generalizability theory will be helpful.

  • Universe
  • Facet

2.3 Statistical inference as severe testing

  • Simple tools: If little or nothing has been done to rule out flaws in inferring a claim, then it has not passed a severe test.
  • Probability as a measure of how capable methods are at uncovering and avoiding erroneous interpretations of data. That’s what it means to view statistical inference as severe testing.
  • Claims may be probable, but terribly tested by the data at hand.

Roland Schäfer is currently working on a statistics textbook for linguists revolving around the notion of severe testing.